疫学は、科学的で正しい判断をするためのもの。
「喫煙者は非喫煙者よりも肺がんの罹患率が4倍である」
このような言葉を一度は耳にしたことがあるでしょう。
さて、何となく理解できるものの、これは本当に正しいことなのでしょうか?
一回の調査をしたら、こういう結果になったけど、再び2回目の調査をしたら違う結果になってしまった。というのでは、信頼ができませんね。
そこで、それを解決するのが「疫学(えきがく)」という考え方と方法です。
疫学は個人ではなく、集団を対象として、病気の発生原因や予防などを研究する公衆衛生学という学問で扱われるものです。
集団を対象とするために統計学を使う必要がありますが、数学の話しはしないので安心して下さい(参考程度に算数は使います)。
疫学は、最初は急性の疾患である伝染病などから私たちを守るために研究されてきましたが、現在では慢性の疾患の生活習慣病をはじめ、集団についてのあらゆる分野で、因果関係の確認に使われています。
なお、集団を研究することは、最終的には、その集団を構成している個々人の健康を守ることになります。
ジョン・スノーの疫学研究
疫学の説明をする前に、歴史的な事件をご紹介します。
1849年に、イギリスのロンドンのブロードストリートでコレラ患者が大量発生しました。
オランダのレーウェンフックが初めて微生物を発見してから150年以上経っても微生物が伝染病の原因であることは明らかになっていませんでした。
その当時、病気は空気の汚れ「瘴気(しょうき)」が原因だとするミアズマ説(miasma theory)というのが信じられていました。
不潔なぞうきんからハエが飛び立ったら、ぞうきんがハエを産んだ(!?)なんてことが信じられていた時代でした。日本では十二代将軍の徳川家慶の時代ですね。
1854年に再びコレラが発生した時、イギリス人医師のジョン・スノウは、瘴気説に疑問を持ち、住民から情報を集め調査を行い、地図上に患者と井戸の存在を書き込みました。
それによって、ブロード・ストリートの井戸がコレラ菌の発生現場であることを特定しました。その井戸水を使用禁止することで、それ以上の流行を防ぐことができました。世界で初めての疫学調査でした。
ドイツの細菌学者ロベルト・コッホがコレラを発見したのは1883年ですから、30年前のできごとです。
この事件でわかったことは、原因が不明の疾患でも疫学的調査により予防が可能であることが示されたことです。
日本では、1883年頃、海軍で脚気が流行していました。
東京慈恵会医科大学の創設者である軍医の高木兼寛(たかきかねひろ)が海軍での兵食改革(洋食+麦飯)を行い、当時なじみの薄かったカレーを海軍の食に取り入れ、脚気を激減させました。脚気という病気の正体がわからないのに麦飯にすることで、スノーと同じように予防をしたことになります。
これは日本で初めて実験疫学的に証明したことで有名な事件です。
この2つのことから、まず、事件が起こると、
・調査をして「仮説」を立てる(記述疫学)。
・次に、その仮説が正しいかを調べ(分析疫学)、
・実行をする(実験疫学)。
という流れが、疫学の手順になりまです。
記述疫学→分析疫学→実験疫学
ただ、記述疫学の結果を分析疫学で分析する前に、「少なくともこれは満たしていなければ仮説としておかしい」と言う基準があります。
つまり、因果関係の確認です。
因果関係というのは、
「Aが起きるとBが起こり、Aが起きなければBは起こらない」
↓
「AがBの原因である」
という関係が成り立つことです。
妥当性を検証する基準はいくつかありますが、一般的なものを述べます(スノーの例を挙げて)。
(1)人、場所、時間の関連に普遍性があるか(関連の一致性)。
例:水道水を飲めば誰でもコレラに罹るのか
(2)効果が定量的かどうか(関連の強固性)
例:水道水を飲めば飲むほどにコレラになる割合が上がるのか
(3)原因のある所に結果があり、結果のある所に原因があるか(関連の特異性)
例:水道水を飲んだ人がコレラに罹り、かつ、コレラ患者は水道水を飲んでいるのか
(4)原因が結果より先に存在すること(関連の時間性)
例:コレラに罹った後から水道水を飲んだだけではないのか
(5)既知の知識体系と矛盾しないか(関連の整合性)
例:水道水やコレラに関するこれまでの研究と仮説との間に整合性はあるか
関連の時間性(原因→結果)は必須ですが、因果関係があった場合に全てこれらの条件が満たされるわけではなく、条件を満たしている場合でも、必ずしも因果関係があるとはいえません。研究の目的に対して疫学研究の妥当性も踏まえて判断する必要があるからです。
コホート研究
分析疫学の1つの手法には、コホート研究( cohort study)があります。
コホート研究とは、ある特定の要因(原因)にさらされた(曝露したといいます)集団(たとえば喫煙習慣群)とさらされていない(曝露していない)集団(たとえば喫煙習慣がない群)を2つのグループに分け、一定期間追跡して、研究対象となる疾病(たとえば肺がん)の発生率を比較することで、要因と疾病発生の関連を調べる観察的研究です。
コホートというのは、一定の期間にわたって追跡される研究目的で構成される人間集団のことをいいます。コホートという言葉は、古代ローマの歩兵隊の単位に由来します。
コホート研究は集団を前向き(将来にわたって)に追跡しているので、曝露から疾病発生までの過程を時間を追って観察することができます。また、その程度を表す指標(危険率など)も求めることができます。
観察の時間的な順序や論理の流れが実験に近く、複数の疾病についての調査が可能であり、特定の曝露の広範な健康影響を調べることができるという利点があります。
一方で、対象としている疾病の発生が稀である場合には、大規模なコホートを長期間追跡する必要があり、時間とコストがかかるという欠点があります。
世界中で大規模なコホート研究が立案され継続しています。
我が国でも、健康に関係するコホート研究は計画的に実行され、その成果を活かせる時期もくることでしょう。
さて、タイトルの
「たばこを吸う人は吸わない人より、4倍肺がんに罹りやすい。」というのは、たばこを吸うことによって吸わない人より肺がんになるリスク(危険性)が何倍になるかという意味です。
これは、コホート研究の結果を踏まえたものです。
例として、肺がん発生数と喫煙について疫学の効果指標を求めてみましょう。
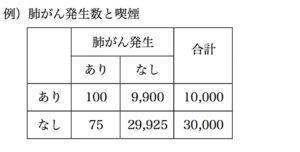
「4万人を対象とした研究で、喫煙歴の有無と肺がんの年間新規発生数を調べた。肺がんの発生は喫煙群の1万に中100人、非喫煙群の3万人中75人であった」とします。
危険性を表す効果の指標として相対危険度(リスク比)があります。つまり、「曝露によって疾病発生のリスクが何倍になるか」を示すものです。
相対危険度 = 曝露群の発生割合 ÷ 非曝露群の発生割合
= ( 100 / 10,000 ) / ( 75 / 30,000 ) = 4
というふうに計算ができますので、非喫煙群と比較して喫煙群では年間の肺がん発生の危険が4倍高いと解釈できます。
また、寄与危険度(リスク差)という指標もあり、「曝露によってリスクがどれだけ増えるか」を求めることができます。
寄与危険度 = 曝露群の発生割合 − 非曝露群の発生割合
= ( 100 / 10,000 ) – ( 75 / 30,000 ) = 0.0075
この例では、このように計算されますので、喫煙がなければ1万にあたり75人の肺がん発症を予防できることを意味します。
これ以外にも分析疫学の手法はありますが、日常的に知っていて欲しいのは、コホート研究です。
ただ、因果関係の強さがこれくらいあるという意味であって、そのものすべてが正しいとは言えません。
喫煙の場合を例にとりましたが、実際には、喫煙でがんになってなくなる方よりも喫煙していない方の方が多いというのが現状です。
たばこには非常に多くの成分が含まれていますので、個々の毒性は確認されているし、身体に外があるのはまず間違いはないでしょう。
しかし、私たちの身体は個人差もあり、非常に複雑なので一律的に結論を出すことは、もう少し時間がかかりそうです。
「疫学調査によると・・・」、「疫学的には・・・」という表現があったら、このような意味を持っているのだと理解して頂ければよいでしょう。
参考文献
・フリー百科事典『ウィキペディア(Wikipedia)』・公衆衛生がみえる(株)メディックメディア
・BD(メディカルデバイス)https://www.bdj.co.jp/safety/articles/ignazzo/hkdqj200000awidd.html
・多目的コホート研究(JPHC):国立研究開発法人 国立がん研究センター 社会と健康研究センター 予防研究グループ
・日本多施設共同コホート研究:J-MICC STUDY
